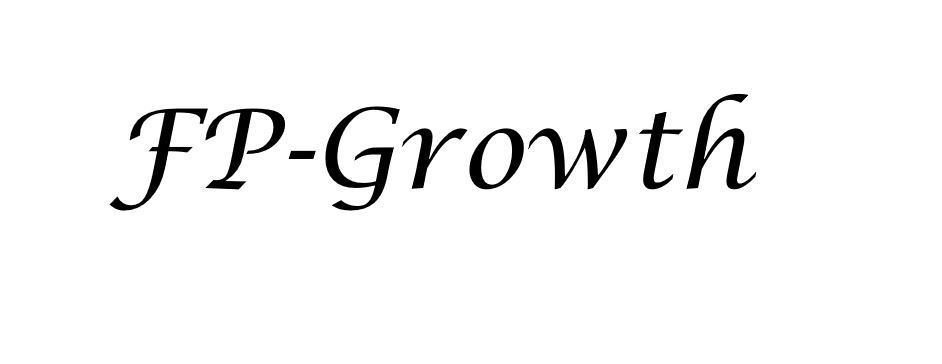你用过搜索引擎吗?输入一个单词或者一个单词的一部分,搜索引擎就会自动补全查询词项。用户甚至事先都不知道搜索引擎推荐的东西是否存在,反而会去查找推荐词项。那么这些推荐词项是如何被搜索引擎找到的?那是因为研究人员使用了FP-growth算法,它是基于Apriori构建的,但完成相同任务时将数据集存储在一个特定的称作FP树的结构之后发现频繁项集或频繁项对,即常在一起出现的元素项的集合FP树。这是一种比Apriori执行速度更快的算法,能高效地发现频繁项集,但不能用于发现关联规则。
FP-growth算法只需要对数据库进行两次扫描,而Apriori算法对于每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁,因此FP-growth算法的速度比Apriori算法快。在小规模数据上,这不是什么问题,但当处理更大数据集时,就会产生较大问题。FP-growth算法只会扫描数据集两次,它不会生成候选项集,其发现频繁项集的基本过程如下:
构建FP树
从FP树中挖掘频繁项集
FP-growth原理 FP-growth算法将数据存储在一种成为FP树的紧凑数据结构中。FP代表频繁模式(Frequent Pattern)。一颗FP树与计算机科学中其他树结构类似,但它通过链接(link)来连接相似元素,被连起来的元素可以看成一个链表。
下面用一个例子来说明,给出一组数据如下:
事物ID
事物中的元素项
001
r,z,h,j,p
002
z,y,x,w,v,u,t,s
003
z
004
r,x,n,o,s
005
y,r,x,z,q,t,p
006
y,z,x,e,q,s,t,m
由此可以生成一棵FP树:
仔细来看这棵FP树,同搜索树不同,一个元素项可以在一棵FP树中出现多次。FP树会存储项集的出现频率,而每个项集会以路径的方式存储在树中。存在相似元素的集合会共享树的一部分。只有当集合之间完全不同时,树才会分叉。树节点上给出集合中单个元素及其在序列中的出现次数,路径会给出该序列的出现次数。相似项之间的链接,即节点链接(node link),用于快速发现相似项的位置。
上图中,元素项z出现了5次,集合{r, z}出现了1次。于是可以知道:z一定是自己本身或者和其他符号一起出现了4次。再看看其他可能,集合{t, s, y, x, z}出现了2次,集合{t, r, y, x, z}出现了1次。元素项z的右边是5,表示z出现了5次,其中刚才已经给出了4次出现,所以它一定单独出现过1次。005号记录是{y, r, x, z, q, t, p},那么q、p去哪儿了呢?
这里使用第11章给出的支持度定义,该指标对应一个最小阈值,低于最小阈值的元素项被认为是不频繁的。若将最小支持度设为3,然后应用频繁项分析算法,就会获得出现3次或3次以上的项集。图中FP树的最小支持度是3,因此p、q并没有出现在树中。
FP-growth算法的工作流程:首先构建FP树,然后利用它来挖掘频繁项集。为了构建FP树,需要对原始数据集扫描两遍。第一遍对所有元素项的出现次数进行计数。记住Apriori原理:如果某元素是不频繁的,那么包含该元素的超集也是不频繁的,所以就不需要考虑超集。数据库的第一遍扫描用来统计出现的频率,第二遍扫描中只考虑那些频繁元素。
构建FP树 首先先用一个容器来保存FP树。
创建FP树的数据结构 创造一个类保存树的每个节点,创建文件fpGrowth.py并加入以下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class treeNode : def __init__ (self, nameValue, numOccur, parentNode) : self.name = nameValue self.count = numOccur self.nodeLink = None self.parent = parentNode self.children = {} def inc (self, numOccur) : self.count += numOccur def disp (self, ind=1 ) : print(' ' *ind, self.name, ' ' , self.count) for child in self.children.values() : child.disp(ind+1 )
上面的程序给出了FP树中节点的类定义。类中包含用于存放节点名字的变量和1个计数值,nodeLink变量用于链接相似的元素项(参考上图中的虚线)。类中还使用了父变量parent来指向当前节点的父节点。通常情况并不需要这个变量,因为通常是从上往下迭代访问节点的。如果需要根据给定叶子节点上溯整棵树,这时候就需要指向父节点的指针。最后,类中还包含一个空字典变量,用于存放节点的子节点。
运行一下如下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 >>> import fpGrowth>>> rootNode = fpGrowth.treeNode('pyramid' ,9 ,None )>>> rootNode.children['eye' ] = fpGrowth.treeNode('eye' ,13 ,None )>>> rootNode.disp() pyramid 9 eye 13 >>> rootNode.children['phoenix' ]=fpGrowth.treeNode('phoenix' ,3 ,None )>>> rootNode.disp() pyramid 9 eye 13 phoenix 3
构建FP树 除上图给出的FP树之外,还需要一个头指针表来指向给定类型的第一个实例。利用头指针表,可快速访问FP树中一个给定类型的所有元素。下图给出了一个头指针表的示意图。
这里使用一个字典作为数据结构来保存头指针表。除了存放指针外,头指针表还可以用来保存FP树中每类元素的总数。
第一次遍历数据集会获得每个元素项的出现频率。接着去掉不满足最小支持度的元素项,再来构建FP树。在构建时,读入每个项集并将其添加到一条已经存在的路径中。如果该路径不存在,则创建一条新路径。每个事务就是一个无序集合。假设有集合{z, x, y}和{y, z, r},那么在FP树中,相同项会只表示一次。为了解决此问题,在将集合添加到树之前,需要对每个集合进行排序。排序基于元素项的绝对出现频率来进行。使用上图中头指针节点值,对前表中数据进行过滤、重排序后的数据显示如下。
事务ID
事务中的元素项
过滤及重排序后的事务
001
r, z, h, j, p
z, r
002
z, y, x, w, v, u, t, s
z, x, y, s, t
003
z
z
004
r, x, n, o, s
x, s, r
005
y, r, x, z, q, t, p
z, x, y, r, t
006
y, z, x, e, q, s, t, m
z, x, y, s, t
在对事务记录过滤和排序之后,就可以构建FP树了。从空集(符号为∅)开始,向其中不断添加频繁项集。过滤、排序后的事务依次添加到树中,如果树中已存在现有元素,则增加现有元素的值;如果现有元素不存在,则向树添加一个分枝。对上表前两条事务进行添加的过程显示如下。
接下来通过代码实现上述过程。在fpGrowth.py加入以下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 def createTree (dataSet, minSup=1 ) : headerTable = {} for trans in dataSet : for item in trans : headerTable[item] = headerTable.get(item, 0 ) + dataSet[trans] for k in list(headerTable.keys()): if headerTable[k] < minSup : del (headerTable[k]) freqItemSet = set(headerTable.keys()) if len(freqItemSet) == 0 : return None , None for k in headerTable : headerTable[k] = [headerTable[k], None ] retTree = treeNode('Null Set' , 1 , None ) for tranSet, count in dataSet.items() : localD = {} for item in tranSet : if item in freqItemSet : localD[item] = headerTable[item][0 ] if len(localD) > 0 : orderedItems = [v[0 ] for v in sorted(localD.items(), key=lambda p : p[1 ], reverse=True )] updateTree(orderedItems, retTree, headerTable, count) return retTree, headerTable def updateTree (items, inTree, headerTable, count) : if items[0 ] in inTree.children : inTree.children[items[0 ]].inc(count) else : inTree.children[items[0 ]] = treeNode(items[0 ], count, inTree) if headerTable[items[0 ]][1 ] == None : headerTable[items[0 ]][1 ] = inTree.children[items[0 ]] else : updateHeader(headerTable[items[0 ]][1 ], inTree.children[items[0 ]]) if len(items) > 1 : updateTree(items[1 ::], inTree.children[items[0 ]], headerTable, count) def updateHeader (nodeToTest, targetNode) : while (nodeToTest.nodeLink != None ) : nodeToTest = nodeToTest.nodeLink nodeToTest.nodeLink = targetNode def loadSimpDat () : simpDat = [ ['r' , 'z' , 'h' , 'j' , 'p' ], ['z' , 'y' , 'x' , 'w' , 'v' , 'u' , 't' , 's' ], ['z' ], ['r' , 'x' , 'n' , 'o' , 's' ], ['y' , 'r' , 'x' , 'z' , 'q' , 't' , 'p' ], ['y' , 'z' , 'x' , 'e' , 'q' , 's' , 't' , 'm' ] ] return simpDat def createInitSet (dataSet) : retDict = {} for trans in dataSet : retDict[frozenset(trans)] = 1 return retDict
运行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 >>> import fpGrowth>>> simpDat = fpGrowth.loadSimpDat()>>> simpDat[['r' , 'z' , 'h' , 'j' , 'p' ], ['z' , 'y' , 'x' , 'w' , 'v' , 'u' , 't' , 's' ], ['z' ], ['r ' , 'x' , 'n' , 'o' , 's' ], ['y' , 'r' , 'x' , 'z' , 'q' , 't' , 'p' ], ['y' , 'z' , 'x' , 'e' , 'q' , 's' , 't' , 'm' ]] >>> initSet = fpGrowth.createInitSet(simpDat)>>> initSet{frozenset({'j' , 'z' , 'h' , 'p' , 'r' }): 1 , frozenset({'u' , 's' , 'x' , 'w' , 'y' , 'v' , 'z' , 't' }): 1 , frozenset({'z' }): 1 , frozenset({'s' , 'x' , 'o' , 'n' , 'r' }): 1 , frozenset({'q' , 'x' , 'y' , 'z' , 't' , 'p' , 'r' }): 1 , frozenset({'s' , 'e' , 'q' , 'x' , 'y' , 'z' , 'm' , 't' }): 1 } >>> myFPtree, myHeaderTab = fpGrowth.createTree(initSet, 3 )>>> myFPtree.disp() Null Set 1 z 5 r 1 x 3 s 2 y 2 t 2 y 1 t 1 r 1 x 1 s 1 r 1
上面给出的是元素项及其对应的频率计数值,其中每个缩进表示所处的树的深度。
从一棵FP树中挖掘频繁项集 有了FP树之后,就可以抽取频繁项集了。这里的思路与Apriori算法大致类似,首先从单元素项集合开始,然后在此基础上逐步构建更大的集合。当然这里将利用FP树来做实现上述过程,不再需要原始数据集了。从FP树中抽取频繁项集的三个基本步骤如下:
从FP树中获得条件模式基;
利用条件模式基,构建一个条件FP树;
迭代重复步骤1、2,直到树包含一个元素项为止。
重点关注第1步,即寻找条件模式基的过程。之后,为每一条件模式基创建对应的条件FP树。最后需构造少许代码来封装上述两个函数,并从FP树中获得频繁项集。
抽取条件模式基 首先从之前保存在头指针中的单个频繁元素项开始。对于每一个元素项,获得其对应的条件模式(conditional pattern base)。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前缀路径(prefix path)。简而言之,一条前缀路径是介于所查找元素项与树根节点之间的所有内容。
回到图2中,符号r的前缀路径是{x, s}、{z, x, y}和{z}。每条前缀路径都与一个计数值关联。该计数值等于起始元素项的计数值,该计数值给了每条路径上r的数目。下表列出了上例当中每一个频繁项的所有前缀路径:
频繁项
前缀路径
z
{}5
r
{x, s}1, {z, x, y}1, {z}1
x
{z}3, {}1
y
{z, x}3
s
{z, x, y}2, {x}1
t
{z, x, y, s}2, {z, x, y, r}1
前缀路径被用于构建条件FP树,但是暂时先不需要考虑这件事。为了获得这些前缀路径,可以对树进行穷举式搜索,直到获得想要的频繁项为止,或使用一个更有效的方法来加速搜索过程。可以利用先前创建的头指针来得到一种更有效的方法。头指针表包含相同类型元素链表的起始指针。一旦到达了每一个元素项,就可以上溯这棵树直到根节点为止。下面代码给出了如何发现前缀路径,将其添加到文件fpGrowth.py中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def ascendTree (leafNode, prefixPath) : if leafNode.parent != None : prefixPath.append(leafNode.name) ascendTree(leafNode.parent, prefixPath) def findPrefixPath (basePat, treeNode) : condPats = {} while treeNode != None : prefixPath = [] ascendTree(treeNode, prefixPath) if len(prefixPath) > 1 : condPats[frozenset(prefixPath[1 :])] = treeNode.count treeNode = treeNode.nodeLink return condPats
运行结果
1 2 3 4 5 6 >>> fpGrowth.findPrefixPath('x' , myHeaderTab['x' ][1 ]){frozenset({'z' }): 3 } >>> fpGrowth.findPrefixPath('z' , myHeaderTab['z' ][1 ]){} >>> fpGrowth.findPrefixPath('r' , myHeaderTab['r' ][1 ]){frozenset({'z' }): 1 , frozenset({'s' , 'x' }): 1 , frozenset({'z' , 't' , 'y' , 'x' }): 1 }
创建条件FP树 对于每个频繁项,都要创建一棵条件FP树。我们会为z、x以及其他频繁项构建条件树。可以使用刚才发现的条件模式基作为输入数据,并通过相同的建树代码来构建这些树。然后,我们会递归地发现频繁项、发现条件模式基,以及发现另外的条件树。举个例子,假定为频繁项 t 创建一个条件FP树,然后对{t, y}、{t, x}、……重复该过程。元素项t的条件FP树的构建过程如下所示。
上图中最初树以空集作为根节点,接着,原始的集合{y, x, s, z}中的集合{y, x, z}被添加进来。因为不满足最小支持度要求,字符s并没有加入进来。类似地,{y, x, z}也从原始集合{y, x, r, z}中添加进来。 元素项s、r是条件模式基的一部分,但它们并不属于条件FP树。单独来看它们都是频繁项,但是在t的条件树中,它们却不是频繁的,也就是说{t, r}、{t, s}是不频繁的。
接下来,对集合{t, z}、{t, x}、{t, y}来挖掘对应的条件树。这会产生更复杂的频繁项集。该过程重复进行,直到条件树中没有元素为止,然后就可以停止了。实现代码很直观,使用一些递归加上之前写的代码即可。具体如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def mineTree (inTree, headerTable, minSup, preFix, freqItemList) : bigL = [v[0 ] for v in sorted(headerTable.items(), key=lambda p:p[1 ][0 ])] for basePat in bigL : newFreqSet = preFix.copy() newFreqSet.add(basePat) freqItemList.append(newFreqSet) condPattBases = findPrefixPath(basePat, headerTable[basePat][1 ]) myCondTree, myHead = createTree(condPattBases, minSup) if myHead != None : print('conditional tree for: ' , newFreqSet) myCondTree.disp() mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
效果如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 >>> freqItems = []>>> fpGrowth.mineTree(myFPtree, myHeaderTab, 3 , set([]), freqItems)conditional tree for : {'s' } Null Set 1 x 3 conditional tree for : {'y' } Null Set 1 z 3 x 3 conditional tree for : {'y' , 'x' } Null Set 1 z 3 conditional tree for : {'t' } Null Set 1 z 3 y 3 x 3 conditional tree for : {'t' , 'y' } Null Set 1 z 3 conditional tree for : {'t' , 'x' } Null Set 1 y 3 z 3 conditional tree for : {'z' , 't' , 'x' } Null Set 1 y 3 conditional tree for : {'x' } Null Set 1 z 3 >>> freqItems[{'r' }, {'s' }, {'s' , 'x' }, {'y' }, {'y' , 'z' }, {'y' , 'x' }, {'z' , 'y' , 'x' }, {'t' }, {'t' , 'z' }, {'t' , 'y' }, {'t' , 'y' , 'z' }, {'t' , 'x' }, {'t' , 'y' , 'x' }, {'z' , 't' , 'x' }, {'z' , 't' , 'y' , 'x' }, {'x' }, {'z' , 'x' }, {'z' }]
示例:从新闻网站点击流中挖掘 下列文件kosarak.dat中包含了将近100万条记录。该文件中的每一行包含某个用户浏览过的新闻报道。一些用户只看过一篇报道,而有些用户看过2498篇报道。用户和报道被编码成整数,所以查看频繁项集很难得到更多的东西,但该数据对于展示FP-growth算法的速度十分有效。
数据前几行如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 1 4 5 6 7 1 8 9 10 11 6 12 13 14 15 16 1 3 7 17 18 11 6 19 20 21 22 23 24 1 25 3 26 3 11 27 6 3 28 7 29 30 31 32 33 34 35 36 37 6 2 38 39 11 27 1 40 6 41 42 43 44 45 46 47 3 48 7 49 50 51
运用FP-growth算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 >>> parsedDat = [line.split() for line in open('kosarak.dat' ).readlines()]>>> initSet = fpGrowth.createInitSet(parsedDat)>>> myFPtree, myHeaderTab = fpGrowth.createTree(initSet, 100000 )>>> myFreqList = []>>> fpGrowth.mineTree(myFPtree, myHeaderTab, 100000 , set([]), myFreqList)conditional tree for : {'1' } Null Set 1 6 107404 conditional tree for : {'3' } Null Set 1 6 186289 11 117401 11 9718 conditional tree for : {'11' , '3' } Null Set 1 6 117401 conditional tree for : {'11' } Null Set 1 6 261773 >>> len(myFreqList)9 >>> myFreqList[{'1' }, {'1' , '6' }, {'3' }, {'11' , '3' }, {'11' , '6' , '3' }, {'6' , '3' }, {'11' }, {'11' , '6' }, {'6' }]
小结 FP-growth算法是一种用于发现数据集中频繁模式的有效方法。FP-growth算法利用Apriori原则,执行更快。Apriori算法产生候选项集,然后扫描数据集来检查它们是否频繁。由于只对数据集扫描两次,因此FP-growth算法执行更快。在FP-growth算法中,数据集存储在FP树中。FP树构建完成后,可以通过查找元素项的条件基及构建条件FP树来发现频繁项集。该过程不断以更多元素作为条件重复进行,直到FP树只包含一个元素为止。
可以使用FP-growth算法在多种文本文档中查找频繁单词。对Twitter源上的某个话题应用FP-growth算法,可以得到一些有关该话题的摘要信息。频繁项集生成还可以用于购物交易、医学诊断和大气研究等。