相似度计算的python实现

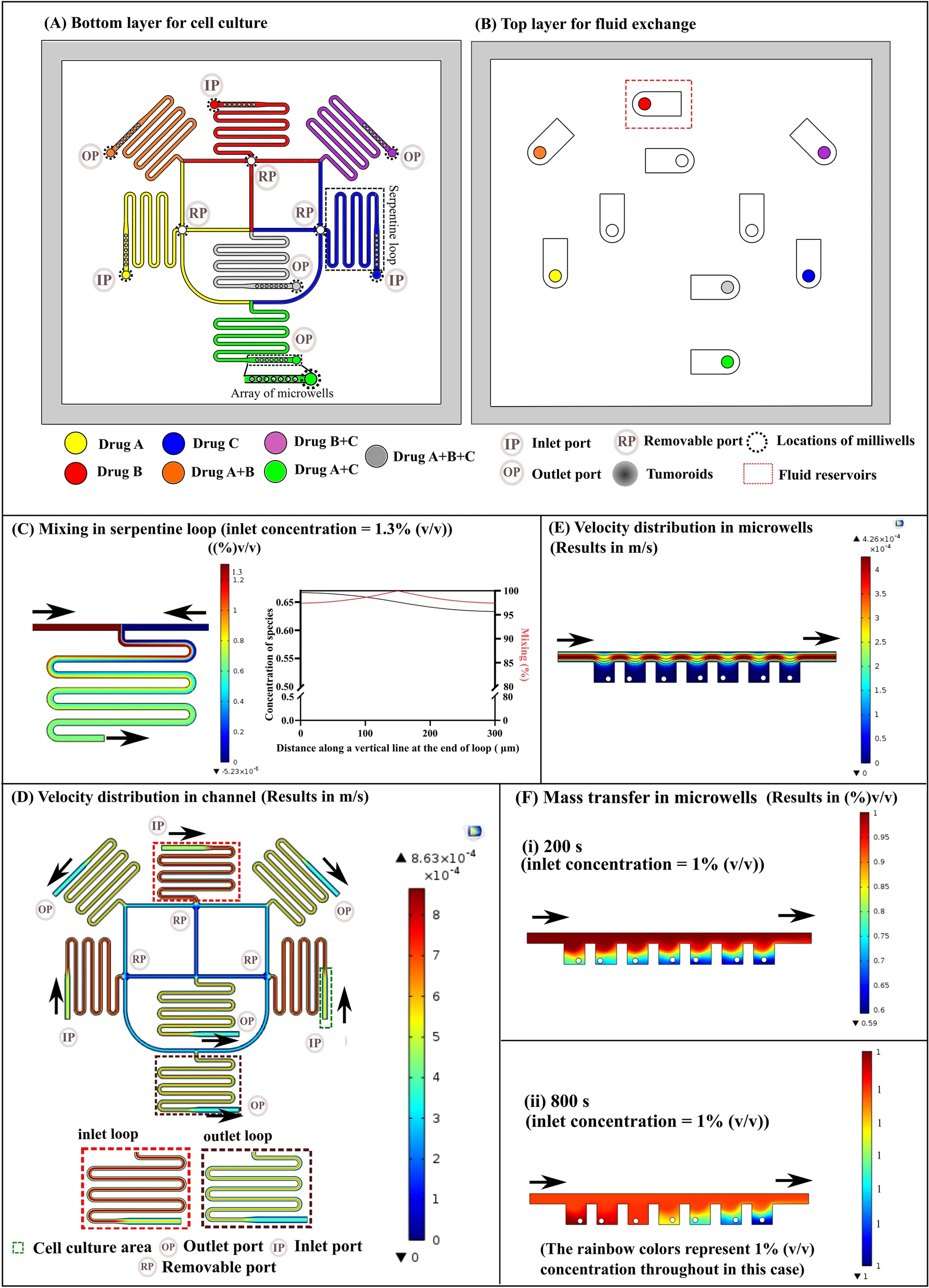
　　在数据挖掘中有很多地方要计算相似度，计算相似度有欧几里德距离、曼哈顿距离、皮尔逊相关度、Jaccard系数和Tanimoto系数等等，这里暂时列出以下几种计算方法。

欧几里得距离

　　欧几里得距离（Euclidean distance）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离），在二维和三维空间中的欧氏距离就是两点之间的实际距离。

　　在Python中，可以调用scikit-learn中现成的轮子实现：

1 2	from sklearn.metrics.pairwise import euclidean_distances distance = euclidean_distances(i1,i2)

　　因为计算是基于各维度特征的绝对数值，所以欧氏距离需要保证各维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标是不适用于欧氏距离的。

　　此外，欧几里得距离是数据上的直观体现，在处理一些受主观影响很大的评分数据时，效果则不太明显；比如，person1对item1,item2 分别给出了2分，4分的评价;person2则给出了4分，8分的评分。通过分数可以大概看出，二个人口味相同，但是第二个人评价稍高。在逻辑上，是可以给出两用户兴趣相似度很高的结论。如果此时用欧式距离来处理，则不能得到这样的结论。即评价者的评价相对于平均水平偏离很大的时候欧几里德距离不能很好的揭示出真实的相似度。

曼哈顿距离

　　曼哈顿距离（Manhattan Distance）又叫出租车距离或者马氏距离，是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

　　对于空间向量(x1,x2,x3,…,xn)和(y1,y2,y3,…,yn)，曼哈顿距离的定义为：

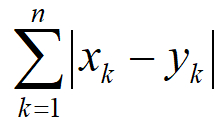
　　同样可以调用scikit-learn中函数：

1 2	from sklearn.metrics.pairwise import manhattan_distances distance = manhattan_distances(i1,i2)

余弦相似度

　　余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫”余弦相似性”。余弦相似度衡量的是维度间取值方向的一致性，注重维度之间的差异，不注重数值上的差异，而欧氏度量的正是数值上的差异性。

　　调用scikit-learn中函数:

1 2	from sklearn.metrics.pairwise import cosine_similarity similarity = cosine_similarity(i1,i2)

　　也可以使用cosine_distances函数，他们的关系是：余弦距离= 1 - 余弦相似度。

皮尔逊相关系数

　　Pearson相关系数是用协方差除以两个变量的标准差得到的，虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但其数值上受量纲的影响很大，不能简单地从协方差的数值大小给出变量相关程度的判断。为了消除这种量纲的影响，于是就有了相关系数的概念。

　　当两个变量的方差都不为零时，相关系数才有意义，相关系数的取值范围为[-1,1]。当相关系数为1时，成为完全正相关；当相关系数为-1时，成为完全负相关；相关系数的绝对值越大，相关性越强；相关系数越接近于0，相关度越弱。

　　可以使用scipy中现有轮子：

1 2	from scipy.stats import pearsonr cor = pearsonr(i1,i2)

　　返回为一个元组，第一项为Pearson相关系数，第二项为p-value。

Jaccard系数

　　Jaccard系数用于比较有限样本集之间的相似性与差异性。当数据集为二元变量时，我们只有两种状态：0或者1，这时候可以使用它来表征相似度。Jaccard系数值越大，样本相似度越高。

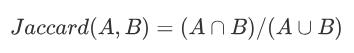
　　在Python中构建函数如下：

def getJaccardCoefficient(p1,p2):
    x1 = p1[p1>0]
    x2 = p2[p2>0]
    si = {}
    for item in list(x1.index):
        if item in list(x2.index):
            si[item] = 1
    n = len(si)
    if n == 0:
        return 0
    return n/(len(x1)+len(x2)-n)

Tanimoto系数

　　Tanimoto系数，又称为广义Jaccard系数，Jaccard系数是xy都是二值向量时的特殊情况，在这种情况下Tanimoto系数就等同Jaccard系数。

　　在Python中构建函数如下：

def getTanimotoCoefficient(p1,p2):
    x1 = p1[p1>0]
    x2 = p2[p2>0]
    si = {}
    for item in list(x1.index):
        if item in list(x2.index):
            si[item] = 1
    n = len(si)
    if n == 0:
        return 0
    sum1 = sum([pow(it,2) for it in x1])
    sum2 = sum([pow(it,2) for it in x2])
    sumco = sum([x1[it]*x2[it] for it in si])
    return sumco/(sum1+sum2-sumco)